Integrated Rate Equations

Integrated Rate Equations

Zero Order Reactions

Zero-order reaction means that the rate of the reaction is proportional to zero power of the concentration of reactants. Consider the reaction,

R→P

Rate=

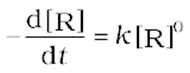
As any quantity raised to power zero is unity

Rate=

d[R] = –kdt

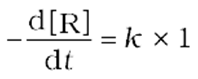
Integrating both sides

[R] = –k t+ I (5)

where I is the constant of integration.

Att= 0, the concentration of the reactant R = [R]₀, where [R]₀ is the initial concentration of the reactant.

Substituting in equation (5)

[R]₀= –k× 0 + I

[R]₀= I

Substituting the value of I in the equation (5)

[R] = -kt+ [R]₀ (6)

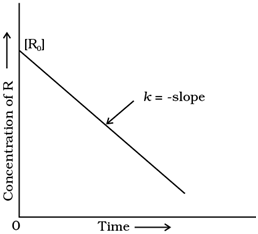
Variation in the concentration vs. time plot for a zero-order reaction

Comparing (6) with the equation of a straight line, y = mx + c, if we plot [R] against t, we get a straight line with slope = –k and intercept equal to [R]₀.

Further simplifying equation (4.6), we get the rate constant,kas

(7)

Zero order reactions are relatively uncommon but they occur under special conditions. Some enzyme catalysed reactions and reactions which occur on metal surfaces are a few examples of zero-order reactions. The decomposition of gaseous ammonia on a hot platinum surface is a zero-order reaction at high pressure.

Rate =k[NH₃]⁰=k

In this reaction, platinum metal acts as a catalyst. At high pressure, the metal surface gets saturated with gas molecules. So, a further change in reaction conditions is unable to alter the amount of ammonia on the surface of the catalyst making rate of the reaction independent of its concentration. The thermal decomposition of HI on gold surface is another example of zero order reaction.

First Order Reactions

In this class of reactions, the rate of the reaction is proportional to the first power of the concentration of the reactant R. For example,

R→P

or

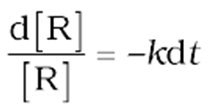
Integrating this equation, we get

ln [R] =–kt+ I (8)

Again, I is the constant of integration and its value can be determined easily.

Whent= 0, R = [R]₀, where [R]₀is the initial concentration of the reactant.

Therefore, equation (8) can be written as

ln [R]₀= –k× 0 + I

ln [R]₀= I

Substituting the value of I in equation (8)

ln[R] = -kt+ ln[R]₀ (9)

Rearranging this equation

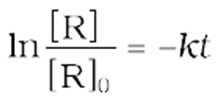
or

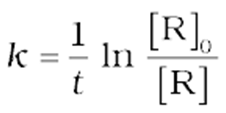(10)

At time t₁from equation (8)

*ln[R]₁= –kt₁+ *ln[R]₀ (11)

At timet₂

ln[R]₂= –kt₂+ ln[R]₀ (12)

where [R]₁and [R]₂are the concentrations of the reactants at timet₁andt₂respectively.

Subtracting (12) from (11)

ln[R]₁– ln[R]₂= –kt₁– (–kt₂)

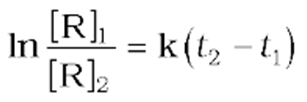(13)

Equation (9) can also be written as

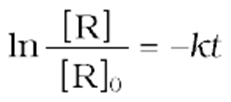
Taking antilog of both sides

[R] = [R]₀e^-kt (14)

Comparing equation (9) with y = mx + c, if we plot ln [R] against t we get a straight line with slope = –k and intercept equal to ln [R]₀

The first-order rate equation (10) can also be written in the form

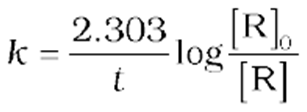(15)

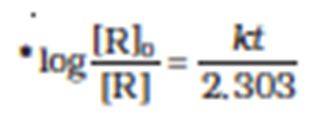
If we plot a graph between log [R]₀/[R] vs t, the slope = k/2.303

Hydrogenation of ethene is an example of a first-order reaction.

C₂H₄(g) + H₂(g)→C₂H₆(g)

Rate =k[C₂H₄]

All natural and artificial radioactive decay of unstable nuclei takes place by first-order kinetics.

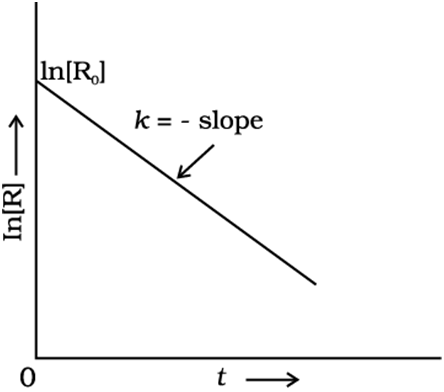
A plot between ln[R] and t for a first-order reaction

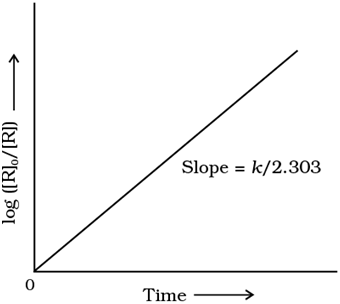
Plot of log [R]₀/[R] vs time for a first order reaction

Rate =k[Ra]

Decomposition of N₂O₅and N₂O are some more examples of first-order reactions.

Let us consider a typical first-order gas phase reaction

A(g)→B(g) + C(g)

Letp_ibe the initial pressure of A andp_t the total pressure at a time ‘t’. An integrated rate equation for such a reaction can be derived as

Total pressurep_t=p_A+p_B+p_C(pressure units)

p_A,p_B,andp_C are the partial pressures of A, B, and C, respectively.

If x atm is the decrease in pressure of A at time t and one mole each of B and C is being formed, the increase in pressure of B and C will also be x atm each.

where p_iis the initial pressure at timet= 0.

p_t= (p_i– x) + x + x =p_i+ x

x = (p_t-p_i)

where,p_A=p_i– x =p_i– (p_t–p_i)

= 2p_i–p_t

k =

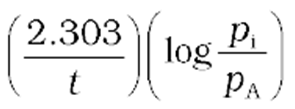(16)

---

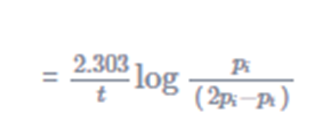
Half-Life of a Reaction

The half-life of a reaction is the time in which the concentration of a reactant is reduced to one-half of its initial concentration. It is represented as t_1/2.

For a zero-order reaction, the rate constant is.

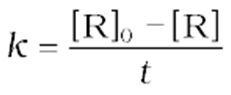
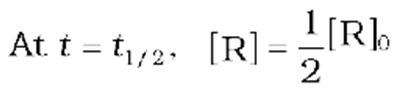
The rate constant at t_1/2becomes

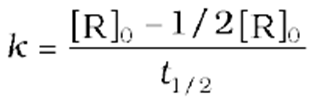
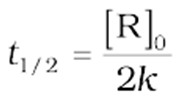
It is clear thatt_1/2for a zero-order reaction is directly proportional to the initial concentration of the reactants and inversely proportional to the rate constant.

For the first-order reaction,

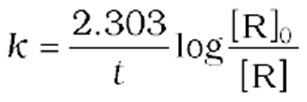
att_1/2

So, the above equation becomes

or

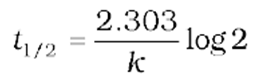
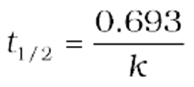
It can be seen that for a first-order reaction, the half-life period is constant, i.e., it is independent of the initial concentration of the reacting species. The half-life of a first-order equation is readily calculated from the rate constant and vice versa.

For zero order reactiont_1/2∝[R]₀. For first-order reaction, t_1/2is independent of [R]₀.

Pseudo-first-order reactions

Pseudo-first-order reactions are not truly first-order but show first-order kinetics under certain conditions. e.g., hydrolysis of ester, inversion of cane sugar

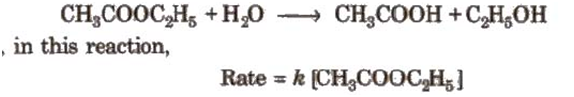
If water is present in excess amounts.